亖Ver.1.2亖
憅杮 揙
97.4.25夵掶=98.4
![]()
亖Ver.1.2亖
憅杮
揙
97.4.25夵掶=98.4
|
拲堄(偆偭偐傝)儈僗 |
|
| 嘆 | 婰崋偺揮婰儈僗丂 亊 佁 亐 亄 佁 亅 亊 佁 亄 |
| 嘇 | 悢抣偺揮婰儈僗丂 俇 佁 侽 俇 佁 俉 |
| 嘊 |
彫悢揰偺揮婰儈僗 32.58 佀 3.258傗 325.8 |
|
寁嶼偺偒傑傝偵娭偡傞娫堘偄丂(惍悢亄彫悢亄暘悢偵嫟捠) |
|
| 嘆-1) | 寁嶼偺弴彉偺娫堘偄 俙亐俛亊俠丂佀 (薪)丂俙亐(俛亊俠) 丂丂摿偵丄(俙亄俢)亐俛亊俠偺傛偆側妵屖偮偒偺応崌偵懡偄 |
| 嘇-2) | 寁嶼偺弴彉偺娫堘偄 俙亄俛亊俠丂佁 (薪)丂(俙亄俛)亊俠 |
| 嘊 | 昅嶼偺偲偒丄忋壓傪偒偪傫偲懙偊側偄偙偲偵傛傞娫堘偄 |
| 嘋 | 懌偟嶼(偐偗嶼)偱偺孞傝忋偑傝偺娫堘偄 丂丂丂 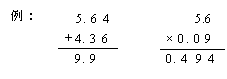 |
| 嘍 | 堷偒嶼偱偺孞傝壓偑傝偺娫堘偄 丂丂丂 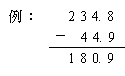 丂丂仸傢傝嶼偵傕尵偊傞 |
| 嘐 | 偐偗嶼偱丄悢偺娫偵侽偑偁傞寁嶼偱偺娫堘偄 丂丂 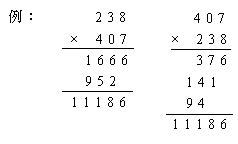 |
| 嘑 |
彍朄偺尨棟(偨傔偟嶼)偺娫堘偄(廳梫) |
|
惍悢寁嶼偺娫堘偄(彫悢亄暘悢偵嫟捠) |
|
| 嘆 |
嬨嬨偺娫堘偄 |
| 嘇 | 戝偒側悢偺寁嶼偱偺侽偺屄悢偺娫堘偄 |
|
彫悢寁嶼偺娫堘偄 |
|
| 嘆 | 彫悢揰偺晅偗曽偺娫堘偄 丂丂丂仸壛尭 佁 忔彍 偺嬫暿偑偮偄偰偄側偄 丂 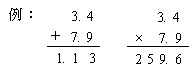 |
| 嘇 |
傢傞悢丄傢傜傟傞悢偺彫悢揰偺堏摦偺娫堘偄 |
| 嘊 |
梋傝偺彫悢揰偺埵抲偺娫堘偄 |
| 嘋 | 巐幪屲擖偟偰彫悢戞俀埵傑偱媮傔傞栤戣偱丄戞俀埵傪巐幪屲擖偟偰偟傑偆娫堘偄 |
| 嘍 |
巐幪屲擖偺偲偒偺彫悢揰埲壓偺侽偺晅偗朰傟偺娫堘偄 |
|
暘悢寁嶼偺娫堘偄 |
|
| 嘆 | 嵟弶偵栺暘偟側偄偨傔丄暘曣巕偑戝偒偔側傝丄栺暘偑偱偒側偄娫堘偄 |
| 嘇 |
捠暘偺巇曽偑敾傜側偄娫堘偄 |
| 嘊 |
偐偗嶼偱懷暘悢偺傑傑偐偗偰偟傑偆娫堘偄 |
| 嘋 | 傢傝嶼偱丄妱傜傟傞悢傪媡悢偵偟偰偟傑偭偨傝丄妱傜傟傞悢傕妱傞悢傕媡悢偵偟偰偟傑偆娫堘偄 丂 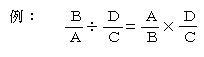 |
| 嘍 |
栺暘偺偟朰傟偺娫堘偄 |
|
媡嶼偺娫堘偄 |
|
| 嘆 | 俙亅仩亖俛丂佀(薪)丂仩亖俙亄俛 |
| 嘇 | 俙亐仩亖俛丂佀(薪)丂仩亖俙亊俛 |
|
挿偄寁嶼栤戣偺娫堘偄 |
|
| 嘆 | 堦晹暘偟偐寁嶼偟側偄偙偲偵傛傞娫堘偄 丂丂丂仸俙亐俛亅俠亐俢亊俤亄俥亊俧 丂丂側偳偱丄亄傗亅偱嬫愗傜傟偨幃傪偦傟偧傟[搰]偲屇傋偽丄偙偺[搰]偛偲偺寁嶼偼梋 丂丂丂敀偱傗傝丄偦偺搒搙丄偦偺寢壥傪揮婰偡傞廗姷傪偮偗偝偣傞偙偲丅偙偺偲偒丄墶偵偮側偘偢偵廲偵廲偵揮婰偡傞偙偲丅 丂丂丂丂丂 丂丂丂丂丂椺丗 丂俙亐俛亅俠亐俢亊俤亄俥亊俧 丂丂丂丂丂丂丂亖 俫 亅 俬 亄 俰 |
| 嘇 |
挿偄幃偺媡嶼偱偺娫堘偄 |
|
亂傑偲傔亃埲忋偐傜丄儈僗偺尨場傪傑偲傔傞偲丄 |
|
| 嘆 |
寁嶼偺偒傑傝傪偟傜側偄偨傔偵婲偒傞儈僗 |
| 嘇 |
偆偭偐傝儈僗
偲 媫偓偡偓偵傛傞儈僗 |
| 嘊 | 寁嶼傪偍偞側傝偵偟偰偄傞儈僗 丂丂丂佀埫嶼偵棅傜偢丄昅嶼傪妋幚偵偟丄偦偺寢壥傪彂偒幨偡暼傪偮偗傞昁梫偑偁傞丅 |
|
亂敪尒曽朄偲懳嶔亃 |
|
| 嘆 | 娫堘偄偺懡偔偼丄寁嶼偺曽朄傪妛廗偟偨偲偒偵丄揙掙偟偨墘廗傪傗偭偰偄側偄偨傔偱偁傞丅捠忢丄妛廗偟偨帪婜(俀乣俁廡娫)偼丄寁嶼捫偗偵側傞傋偒偱偁傞丅 |
| 嘇 |
娫堘偄偺僷僞乕儞偼丄屄惈揑偱偁傞丅偡側傢偪丄侾恖侾恖堎側傞偺偱丄娫堘偄偺僷僞乕儞傪傑偢敪尒偟側偗傟偽側傜側偄丅 偦偺敪尒偼丄杮恖偑峴偆偺偼擄偟偔丄曐岇幰偑傗傞傋偒偱偁傠偆丅 偦偺偨傔偵偼丄侾偮偺栤戣偼傑偲傑偭偨埵抲偱峴偄丄幃傗昅嶼傪巆偟偰偍偔昁梫偑偁傞丅偁偨傝偐傑傢偢僶儔僶儔偵彂偔偲丄娫堘偄傪敪尒偡傞偺偵帪娫偑偐偐傝丄旀傟偰偟傑偆丅偦偟偰丄偦偺寢壥傪丄杮恖偵帵偟丄偦偺庬偺寁嶼偵弌夛偭偨偲偒偵偼丄摿偵拲堄偡傞傛偆偵偝偣傞偙偲偑戝愗偱偁傞丅 |
| 嘊 |
寁嶼偺曽朄偼丄傎傏杮擻揑偵婰壇偟偰偍傝丄廋惓偼晄壜擻偵嬤偄丅偨偩丄帺暘偼偳偺傛偆側偲偒偵娫堘偊傞偺偐偑敾偭偰偍傟偽丄掶惓偼壜擻偱偁傞丅 |
| 嘋 | 摢擼偑怮偰偄傞偲偒偵傗傞傎偆偑丄娫堘偄傕懡偔側傞偺偱丄僷僞乕儞偺敪尒傕偟傗偡偔丄栚妎傑偟傪寭偹偰丄怮婲偒偵傗傞偺偑岲傑偟偄丅 |
| 嘍 |
枅挬艗醾T栤丅梉崗傗栭側偳偼旔偗偨偄丅偨偩偟丄廗偄巒傔偼丄揙掙揑偵傗傝偨偄丅 |
|
亂巙朷拞暿墢K偡傞寁嶼栤戣偺栚埨亃 |
|
| 嘆 | 亄丄亅丄亊丄亐丄乮丂乯o丂乸偺屄悢偵傛傞丅 丂丂仢惞楈丄戝惉丄弔擔媢丂丂丂丂丂丂丂仺俁乣俆屄 丂丂仢悮嶳丄嬥忛丄柤屆壆妛堾丄垽抦仺係乣俈屄 丂丂仢撿嶳抝巕丄廼摽丂丂丂丂丂丂丂丂丂 仺俆乣俉屄 丂丂仢撿嶳彈巕丄戧丄搶奀丂丂丂丂丂丂 仺俈乣10屄 |
|
亂寁嶼偵偙偩傢傞棟桼亃 |
|
| 嘆 | 擭枅偵惗搆偺寁嶼椡偑棊偪偰偄傞傛偆偵巚傢傟傞丅偦偺尨場偼丄 丂丂丂鶣)墘廗検偺晄懌偲庤敳偒 丂丂丂鶤)僼僅乕儅儖偵偟偨偑偭偰寁嶼偟側偄 偨傔偱偁傞丅 |
| 嘇 |
寁嶼椡偑庛偄偲丄寁嶼栤戣偺傒偵巭傑傜偢丄暥復戣傗恾宍栤戣偵傕塭嬁偟丄嶼悢慡懱偱偺幐揰偑戝偒偄丅 |
| 嘊 | 擖帋偵偍偗傞壢栚枅偺崌奿幰偲庴尡惗偺暯嬒揰偺奿嵎偼丄嶼悢偑嵟傕戝偒偔丄傛偭偰嶼悢偑崌斲傪寛偡傞壜擻惈偑嬌傔偰崅偄丅 |
| 嘋 | 崌斲偑寛偡傞偺偼丄係嫵壢係侽侽揰擖帋偱侾侽揰乣俀侽揰偺斖埻撪偱偁傞丅寁嶼偑惓偟偔偱偒傞偩偗偱丄侾侽揰偺壛揰偼壜擻側偼偢偱偁傞丅偦偺侾侽揰偵偙偩傢傝偨偄丅 |