| 数学は(受験)算数の進化形 |
| =事例= |
| 数学は(受験)算数の進化形 |
| =事例= |
| =まとめ= 算数と数学の相違点 |
|
| 算数 | 数学 |
| 手工業 マニュファクチャ →職人芸 |
機械工業 オートメーション →作業員 |
| 具体的 | 抽象的 |
| 個別対応 | 一般化 |
| 有限の世界 | 無限の世界 |
| =算数は個別、数学は一般化= |
| ★負の数の拡張によって、一般化される事例 |
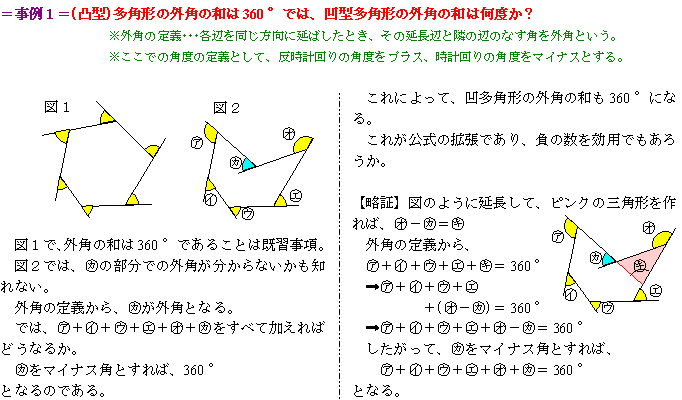
| 負の数は、単なる計算に留まらない。負の数の拡張によって、「100円の損失」
を 「−100円の利益」 と読み替えることで、「利益」と「損失」という2つの言葉を使わずに数量関係が表現されることになる。 その利便さは、図形の公式にも援用される。ここでは、その例を提示しておこう。 なお、数学においては、すべての事柄を【定義】によって処理することになることを理解しておこう。 この【定義】の考え方は、古代ギリシャの【ユーグリッド原論】に遡る。 【定義】がなければ、他者との会話が成立しないからでもある。 |
 |
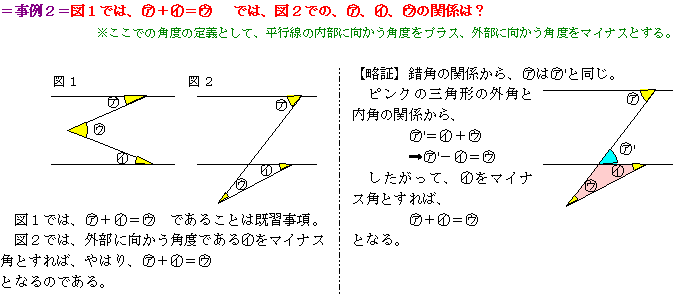 |
| ★文字式(方程式)によって、一般解となる事例 |
|
★文字式(方程式)によって、不定方程式(条件不足の問題)は一般解として提示される 【解説】 ★場合の数 |
| =算数は有限、数学は無限 (高校数学) = |
| ★数列 ★ |